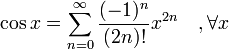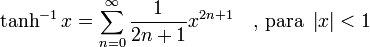sábado, 27 de febrero de 2010
Final
Aquí les dejo el link :
https://sites.google.com/site/ittmatematicasii/
domingo, 13 de diciembre de 2009
Sucesiones y series
 En otras palabras, una sucesión es un conjunto de cosas (normalmente números) una detrás de otra, en un cierto orden. Si la sucesión sigue para siempre se dice que es una sucesión infinita,
En otras palabras, una sucesión es un conjunto de cosas (normalmente números) una detrás de otra, en un cierto orden. Si la sucesión sigue para siempre se dice que es una sucesión infinita,
si no es una sucesión finita.
En matemáticas, una sucesión es el nombre matemático que hace referencia a una lista
infinita de números. En una lista podemos hablar de primer término,
segundo término, etc., que corresponden a la posición que ocupan en
dicha sucesión.
Podemos formalizar todo esto un poco más: podemos asociar cada número
entero positivo n con un número real xn, y el conjunto ordenado:
define una sucesión infinita. Observad que cada término de la sucesión
tiene asignado un número entero positivo (el puesto que ocupa en la lista)
y podemos hablar del primer término (x1), del segundo término (x2) y,
en general, del término n-ésimo (xn). Cada término (xn) tiene un término
siguiente (xn+1), por lo que, en consecuencia, no hay último término.
Una sucesión de números reales es una aplicación h de los números
naturales IN en el conjunto IR de los números reales:
h : IN → IR
n _→ h(n) = xn
La imagen de n recibe el nombre de término n-ésimo o término
general de la sucesión.
Límite finito de una sucesión
Consideremos la sucesión an = 1/n.
a1 = 1
a2 = 1/2 = 0.5
a3 = 1/3 ≈ 0.33
a4 = 1/4 = 0.25
a5 = 1/5 = 0.2
a6 = 1/6 ≈ 0.17
a7 = 1/7 ≈ 0.14
a8 = 1/8 ≈ 0.12
a9 = 1/9 ≈ 0.11
a10 = 1/10 = 0.1
A medida que aumenta n, los términos de la sucesión son cada vez más cercanos a 0. Si representamos los términos como puntos en una línea, esto significa que los puntos an se apiñan cada vez más cerca del punto 0 conforme n crece.

Se dice que an tiende a 0, o que tiene límite 0.
Se expresa simbólicamente por:
Definición
Límite finito
lim an = a <=> para todo ε>0 existe N natural / para todo n > N
Para cualquier número positivo ε, por pequeño que sea, podemos encontrar un natural N suficientemente grande tal que a partir del índice N en adelante se tiene que
Es decir, si tomamos un entorno de a de cualquier radio siempre habrá un subíndice N tal que desde N en adelante todos los términos de la sucesión pertenecen a dicho entorno.
Límite infinito de una sucesión
Consideremos la sucesión an = n2.
a1 = 1
a2 = 4
a3 = 9
a4 = 16
...
a10 = 100
...
a100 = 10.000
Al crecer n, an no tiende a un límite definido, sino que crece más allá de toda cota. Se dice que an tiende a infinito.
Definición
Límite infinito
lim an = +inf <=> para todo K>0 existe N natural / para todo n > N an > K.
Para cualquier número positivo K (tan grande como se quiera), podemos encontrar un natural N, tal que aN y todos los términos siguientes son mayores que K. Esto quiere decir que an puede hacerse mayor que cualquier cota, con tal de que n sea lo suficientemente grande.
Del mismo modo se define lim an = -inf <=> para todo K<0> N an < style="font-size:130%;">Sucesiones monótonasVolvemos a las sucesiones del tema anterior, y consideramos las sucesiones
de t´ermino general xn = 1
n, yn = n y zn = sinn.

Sucesiones monótonas
Volvemos a las sucesiones del tema anterior, y consideramos las sucesiones
de término general xn = 1
n, yn = n y zn = sinn.



Tal y como se observa en los gráficos, la sucesión xn decrece de manera
indefinida, yn crece indefinidamente y zn ni crece ni decrece.
.
verifica que xn ≤ xn+1.
• Una sucesión {xn} es estrictamente creciente si para todo n ∈ IN
se verifica que xn <> xn+1.
Sucesiones acotadas
Consideramos las sucesiones de término general xn = 1
n, yn = n y zn = sinn
y las representamos gráficamente:
 A partir de los gráficos podemos observar cómo la sucesión y n crece de
A partir de los gráficos podemos observar cómo la sucesión y n crece de
forma indefinida, mientras que los valores xn y zn nunca están por encima
de 1. Así, xn y zn son sucesiones acotadas; por el contrario, yn es no acotada.
Una sucesión está acotada si existe un número K tal que los valores que
toma la sucesión nunca superan el valor K.
|xn| ≤ K ∀n ∈ IN.
Entonces, K es una cota de la sucesión {xn}.
- Suma de una serie geométrica, es decir, una serie a1 + a2 + a3 + ... en la que los términos forman una secuencia geométrica.
- La suma de los primeros n términos se puede obtener de la siguiente manera:
Sn = a1 + a2 + a3 + ...an = a1 + a1r + a1r2 + ... + a1rn-1 = a1 (rn - 1)/(r - 1) -
en la que r es la relación común.
- En una sucesión geométrica cada término se calcula multiplicando el anterior por un número fijo.
Los elementos de la sucesion son de la forma an=rn, donde r <> 0, 1.
b. Ejemplos
I. Ajedresista: 1+2+4+8+16+…+2^63
II. Resolucion de forma general de la serie geometrica
III. Aplicacion en la serie (1/2)0+(1/2)1+(1/2)2+…+(1/2)nSerie aritmética
Una serie aritmética o progresión aritmética es una sucesión de números racionales en la que cada termino se obtiene a partir del anterior sumándole un número fijo.
Para indicar el término fijo que se va sumando suele usarse la letra d. Se expresan de la forma an que recibe el nombre de término. n es el indice, e indica la posición que ocupa en la sucesión.
Ejemplo:
d = 3
a1 = 5
a2 = a1 + d = 8
a3 = a2 + d = 11
a4 = a3 + d = 14Término general
El término general es la fórmula que nos permite obtener cualquier término de la sucesión conociendo la posición que ocupa dicho término de la sucesión.
Si observamos el ejemplo anterior observamos que:
a3 = a2 + d = 11
Si sustituimos a2 por a2 = a1 + d = 8 obtenemos:
a3 = a1 + d + d = 11
O lo que es lo mismo:
a3 = a1 + d + d = 11
Si seguimos nos daremos cuenta que siempre se cumple:
an = ak + (n − k)dProgresiones crecientes y decrecientes
Son crecientes aquellas sucesiones en las que d es mayor que 0d > 0
Son decrecientes aquellas sucesiones en las que d es menor que 0
d <>
Si d es igual a 0 la progresión es constante.La sumatoria tiene unas propiedades que se nombraran a continuación:
- para n entero positivo y c constante, se cumple

- Para k entero positivo
 conjunto de numeros reales y c constante real,se cumple
conjunto de numeros reales y c constante real,se cumple

- Para k entero positivo
 conjunto de numeros reales y c constante real,se cumple
conjunto de numeros reales y c constante real,se cumple

- Para k entero positivo
 conjunto de numeros reales y c constante real,se cumple
conjunto de numeros reales y c constante real,se cumple

Estas propiedades se deducen de la las leyes asociativa y conmutativa de la adicion.
Serie de potencias
Una serie de potencias alrededor de x=0 es una serie de la forma:
Una serie de potencias alrededor de x=a es una serie de la forma:
En el cual el centro es a, y los coeficientes cn son constantes.
cnEjemplos:
- La serie geométrica
 es una serie de potencias absolutamente convergente si | x | <> y divergente si | x | > 1 ó | x | = 1
es una serie de potencias absolutamente convergente si | x | <> y divergente si | x | > 1 ó | x | = 1
- La serie de potencias
 es absolutamente convergente para todo
es absolutamente convergente para todo 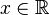
 solamenteconverge para x = 0
solamenteconverge para x = 0

En pocas palabras, para derivar unaserie de potencias es necesario conocer su radio de convergencia,.
Representación de una función en series de potencia
Representación de una función en serie de potencial
Básicamente se analiza la función en serie como lo harías en cualquier función, en el siguiente caso se parece a una función racional lineal, por lo que el resultado es una hipérbola equilátera.



En matemáticas, la serie de Taylor de una función f(x) infinitamente derivable (real o compleja) definida en un intervalo abierto (a-r, a+r) se define como la siguiente suma:


Aquí, n! es el factorial de n y f (n)(a) indica la n-ésima derivada de f en el punto a.
Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor. Una función es analítica si y solo si se puede representar con una serie de potencias; los coeficientes de esa serie son necesariamente los determinados en la fórmula de la serie de Taylor.
Si a = 0, a la serie se le llama serie de Maclaurin.
Esta representación tiene tres ventajas importantes:
- La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.
- Se puede utilizar para calcular valores aproximados de la función.
- Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible.
La serie de Taylor de una función f de números reales o complejos que es infinitamente diferenciable en un entorno de números reales o complejos a, es la serie de potencias:
que puede ser escrito de una manera más compacta como
Series de Taylor notables
A continuación se enumeran algunas series de Taylor de funciones importantes. Todos los desarrollos son también válidos para valores complejos de x.Función exponencial y logaritmo natural
Serie geométrica
Teorema del binomio
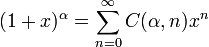 para todo
para todo 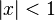 y cualquier
y cualquier  complejo
complejo
Funciones trigonométricas
-
- Donde Bs son los números de Bernoulli
- Donde Bs son los números de Bernoulli
Funcines hiperbólicas
Función W de Lambert

Fuentes:
http://cv.uoc.es/cdocent/A2TQIGW2OHGMOTQC4XAE.pdf
http://www.disfrutalasmatematicas.com/algebra/sucesiones-series.html
http://www.branchingnature.org/Sucesiones_Series_Dario_Sanchez.pdf
http://matematica.50webs.com/sucesiones.html
http://www.gfc.edu.co/estudiantes/anuario/2001/sistemas/halime/hsj/hsj.html
http://www.mitecnologico.com/Main/MatematicasI
http://www.dim.uchile.cl/~docencia/calculo_dif/material/presentacion_semana/presenta_sem15_calcdiff.pdf
http://es.wikipedia.org
http://www.itescam.edu.mx/principal/sylabus/fpdb/recursos/r7009.DOC -
http://www.itescam.edu.mx/principal/sylabus/fpdb/recursos/r7003.DOC -